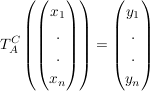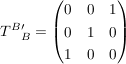TransformationsmatrixDie Transformationsmatrix
Beschreibung
In einem Vektorraum V mit den Basen C und A ist die Transformationsmatrix 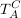 diejenige Matrix, die einen Vektor v aus V, der in Basisgestalt C gegeben ist, gleich (identisch) lässt aber ihn in Basisgestalt A umwandelt. diejenige Matrix, die einen Vektor v aus V, der in Basisgestalt C gegeben ist, gleich (identisch) lässt aber ihn in Basisgestalt A umwandelt.
D.H es soll Folgendes gelten:
 und und 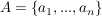 und und 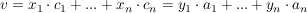 die Basisdarstellungen von v. die Basisdarstellungen von v.
Dann: 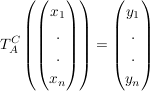
Invertierung
es gilt : 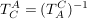
denn 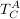 soll einen Vektor bzgl A in denselben bzgl C verwandeln soll einen Vektor bzgl A in denselben bzgl C verwandeln
und 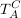 macht gerade das Umgekehrte (inverse) dazu. macht gerade das Umgekehrte (inverse) dazu.
(dies ist kein ausreichender Beweis, sondern nur schlagendes Argument)
Besonderheit
Es sei eine Basis A gegeben (zum Beispiel Standardbasis)
und eine weitere Basis B sei gegeben, wobei jeder Basisvektor 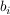 gegeben sei als Linearkombination der Basisvektoren gegeben sei als Linearkombination der Basisvektoren 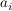 aus A. aus A.
gesucht : 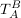
wenn man 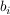 reinsteckt aber bzgl B also reinsteckt aber bzgl B also 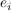 (der i-te Einheitsvektor) soll man die Darstellung bzgl A bekommen, aber die ist ja nun gerade gegeben, d.h. die Spalten sind genau die gegebenen Linearkombinationen. (der i-te Einheitsvektor) soll man die Darstellung bzgl A bekommen, aber die ist ja nun gerade gegeben, d.h. die Spalten sind genau die gegebenen Linearkombinationen.
Beispiel : n=3 und 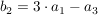 gegeben, dann ist die zweite Spalte von gegeben, dann ist die zweite Spalte von 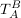 gerade gerade  (anderen Spalten analog) (anderen Spalten analog)
gesucht : 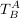
dies würde sich nicht so einfach direkt erkennen lassen, denn wir suchen die Basisdarstellung von A in B.
Weil wir aber gerade das umgekehrte gegeben haben, berechnet man zuerst 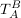 ; ;
und danach die Inverse zum Beispiel mit Gauß-Jordan.
Hinweis:
wenn A und C bzgl einer dritten Basis gegeben sind (z.B. Standardbasis) , dann ist die Transformationsmatrix mit 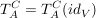 eigentlich eine Koordinatentransformation und damit selbst ein Spezialfall der Transformationsformel (in diesen Fällen muss man Letztere also mehrfach anwenden um die Transformationsmatrizen zu erhalten und dann zum Schluß die eigentlich gesuchte Darstellungsmatrix). eigentlich eine Koordinatentransformation und damit selbst ein Spezialfall der Transformationsformel (in diesen Fällen muss man Letztere also mehrfach anwenden um die Transformationsmatrizen zu erhalten und dann zum Schluß die eigentlich gesuchte Darstellungsmatrix).
einfaches Beispiel
gegeben eine Basis 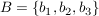 und die Basis und die Basis 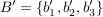 mit mit 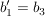 , , 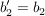 und und 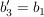
(also erste und dritte Komponente vertauscht, siehe auch : Permutationsmatrix)
dann ist 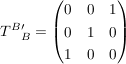 , denn wenn man z.B. , denn wenn man z.B. 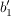 bzgl bzgl 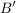 (also (also  ) reinsteckt, soll ) reinsteckt, soll 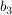 bzgl bzgl 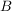 (also (also  ) rauskommen. ) rauskommen.
Matheraum Links
![Link auf "http://www.matheplanet.com/matheplanet/nuke/html/article.php?sid=581" [link]](/images/popup.gif) guter Artikel (MathePlanet) guter Artikel (MathePlanet)
|