KurvendiskussionDefinition Kurvendiskussion
Schule
... nennt man die ausführliche Untersuchung von Funktionen und ihren Graphen.
Man untersucht das Verhalten einer Funktion für sehr große oder sehr kleine x,
prüft,
sucht die Schnittpunkte mit den Koordinatenachsen (= Nullstellen),
ermittelt die Extrempunkte und Wendepunkte.
Bevor man eine Zeichnung macht, sollte man sich auch noch überlegen,
in welchen Bereichen eine Funktion monoton steigt oder fällt.
Dabei nutzt man die Methoden der Ableitungen einer Funktion und interpretiert sie:
Nullstellen der 1. Ableitung sind Kandidaten für Extremstellen,
Nullstellen der 2. Ableitung sind Kandidaten für Wendestellen.
Daraus ergibt sich folgendes Schema:
- Definitions- und Wertebereich, falls nicht schon angegeben oder trivial
- Symmetrie zu y-Achse (Achsensymmetrie) oder Ursprung (Punktsymmetrie)
- Verhalten für
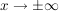
- bei gebrochen-rationalen Funktionen:
- Definitionslücken, Asymptoten, (asymptotische Näherungsfunktion)
- Untersuchung der Nullstellen des Nenners: Polstellen
- Nullstellen
- Ableitungen
- Extremstellen, -punkte
- Wendestellen, -punkte, (Sattelpunkte)
- Graph zeichnen
Zum Zeichnen des Funktionsgraphen empfehlen wir ![Link auf "http://www.funkyplot.de" [link]](/images/popup.gif) FunkyPlot FunkyPlot
ausführliche Kurvendiskussion bei ![Link auf "http://de.wikipedia.org/wiki/Kurvendiskussion" [link]](/images/popup.gif) Wikipedia Wikipedia
| 