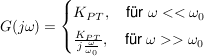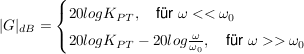FrequenzkennlinienFrequenzkennlinien
Anhand des Frequenzkennlinien- und des Wurzelortskurvenverfahrens ist ein Entwurf oder eine Analyse für einen Regelkreis möglich.
Der Ausgangspunkt ist wie beim Ortskurvenverfahren der Frequenzgang 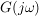 . Er wird hierbei in die zwei Bestandteile: Betrag . Er wird hierbei in die zwei Bestandteile: Betrag 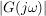 und Phase und Phase 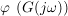 zerlegt und üblicherweise in zwei getrennten Diagrammen dargestellt. zerlegt und üblicherweise in zwei getrennten Diagrammen dargestellt.
Eine Besonderheit liegt jedoch darin vor, dass der Wert des Betrages im dekadischen Logarithmus und mit dem Faktor 20 versehen ist. Man gleicht hier (um Rechenvorteile ausnutzen zu können) den Betrag der Form "Dezibel" [dB] an. Die Phase bleibt unangetastet.
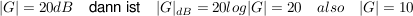
ist jedoch
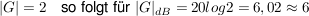
Kennlinien von Übertragungsgliedern:
P-Glied:
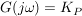
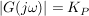
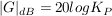
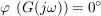
I-Glied:
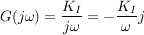
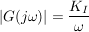
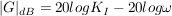
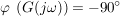
D-Glied:
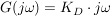
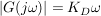
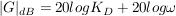
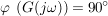
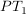 -Glied: -Glied:
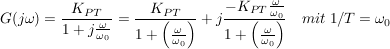
es gilt dann annähernd:
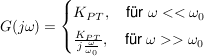
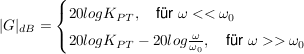
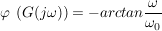
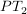 -Glied: -Glied:
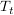 -Glied: -Glied:
zur Übersicht Regelungstechnik
|