Betrag
Schule
Definition Betrag einer reellen Zahl
Der Betrag einer reellen Zahl 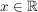 (im Zeichen |x|) ist wie folgt definiert: (im Zeichen |x|) ist wie folgt definiert:
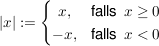
Beispiele.
1.) Wegen 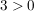 ist |3|=3. ist |3|=3.
2.) Wegen 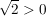 ist ist 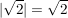 . .
3.) Es gilt |0|=0.
4.) Es gilt  , also ist |-7|=-(-7)=7. , also ist |-7|=-(-7)=7.
5.) Es gilt ![$ -\wurzel[7]{1023}<0 $ $ -\wurzel[7]{1023}<0 $](/teximg/7/6/00392067.png) , also ist , also ist ![$ |-\wurzel[7]{1023}|=-(-\wurzel[7]{1023})=\wurzel[7]{1023} $ $ |-\wurzel[7]{1023}|=-(-\wurzel[7]{1023})=\wurzel[7]{1023} $](/teximg/4/8/00387184.png) . .
Bemerkungen.
1.) Für alle 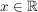 gilt gilt 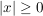 . Denn: . Denn:
1. Fall: Für  gilt gilt 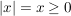 . .
2. Fall: Für 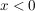 gilt gilt
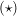 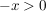
und damit folgt:
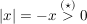 , also insbesondere , also insbesondere 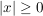 . .
Damit gilt 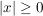 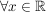 in allen Fällen,und damit ist die Behauptung gezeigt! in allen Fällen,und damit ist die Behauptung gezeigt!
2.) Auf der Zahlengeraden gibt der Betrag einer reellen Zahl x den Abstand der Zahl x zur Zahl 0 an.
3.) Für jede reelle Zahl x gilt die Gleichung:
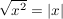 , denn: , denn:
1. Fall: Für 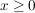 gilt gilt 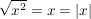 . .
2. Fall: Für 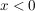 gilt gilt
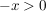 , und deswegen folgt: , und deswegen folgt:
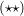 -x=|x|. -x=|x|.
Somit folgt:
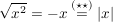 . .
Damit gilt 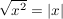 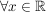 in allen Fällen und die Behauptung ist gezeigt (siehe auch Quadratwurzel einer reellen Zahl). in allen Fällen und die Behauptung ist gezeigt (siehe auch Quadratwurzel einer reellen Zahl).
Universität
Definition Betrag
Seien 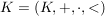 ein geordneter Körper und ein geordneter Körper und 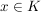 sowie sowie 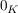 das Nullelement von K. Dann heißt: das Nullelement von K. Dann heißt:
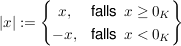
der (absolute) Betrag von x.
Bemerkungen.
Es sei stets 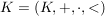 ein geordneter Körper und es sei ein geordneter Körper und es sei 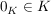 das zugehörige Nullelement. Dann gelten: das zugehörige Nullelement. Dann gelten:
1.) 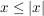 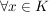 , ,
denn:
1.Fall: 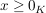 . Dann gilt: . Dann gilt:
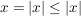
2.Fall:
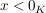 . Dann gilt: . Dann gilt:
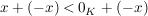
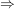
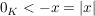
und es folgt:
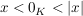 , also insbesondere: , also insbesondere:

2.) Die Dreiecksungleichung:
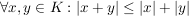 , ,
denn:
1.Fall: 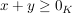 . Dann gilt: . Dann gilt:
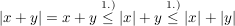
2.Fall:  . Dann gilt: . Dann gilt:
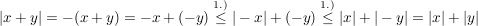
3.) Es gilt 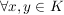
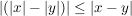 , ,
denn:
Es gilt:
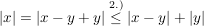
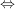
 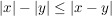
und analog sieht man:
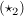 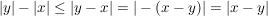
Aus 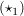 und und 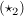 folgt die Behauptung. folgt die Behauptung.
4.) 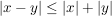 , ,
denn:

5.) Seien 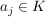 (j=1,...,n). Dann gilt: (j=1,...,n). Dann gilt:
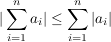 . .
Beweis:
Per Induktion:
Induktionsanfang:
Für n=1 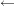 klar klar
Induktionsschritt:
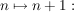
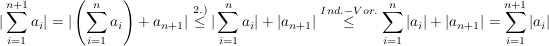

6.) Es gilt die Bernoulli-Ungleichung.
| 