Raum für Mathematik Offene Informations- und Nachhilfegemeinschaft Für Schüler, Studenten, Lehrer, Mathematik-Interessierte.
	Hallo Gast! [ einloggen \| registrieren ]
	Startseite · Forum · Wissen · Kurse · Mitglieder · Team · Impressum

Forenbaum

Gezeigt werden alle Foren bis zur Tiefe 2

Navigation

Startseite...
Neuerdings beta neu
Forum...
vorwissen
	Einstieg

	Index aller Artikel

	Hilfe / Dokumentation
	Richtlinien
	Textgestaltung
vorkurse...
Werkzeuge...
Nachhilfevermittlung beta...
Online-Spiele beta
Suchen
Verein...
Impressum

Das Projekt

Server und Internetanbindung werden durch Spenden finanziert.

Organisiert wird das Projekt von unserem Koordinatorenteam.

Hunderte Mitglieder helfen ehrenamtlich in unseren moderierten Foren.

Anbieter der Seite ist der gemeinnützige Verein "Vorhilfe.de e.V.".

Partnerseiten

Weitere Fächer:

Vorhilfe.de

FunkyPlot: Kostenloser und quelloffener Funktionenplotter für Linux und andere Betriebssysteme

Startseite > Bruchrechnen

Foren für weitere Studienfächer findest Du auf www.vorhilfe.de z.B. Astronomie • Medizin • Elektrotechnik • Maschinenbau • Bauingenieurwesen • Jura • Psychologie • Geowissenschaften

Bruchrechnen

Mach mit! und verbessere/erweitere diesen Artikel!

Artikel • Seite bearbeiten • Versionen/Autoren

Bruchrechnen

Addition und Subtraktion von Brüchen

Ungleichnamige Brüche werden für Addition und Subtraktion gleichnamig gemacht.
Gleichnamige Brüche werden addiert (oder subtrahiert),
indem man die Zähler addiert (oder subtrahiert) un den Nenner beibehält.

$\bruch{1}{2} + \bruch{3}{4} + \bruch{2}{3} = \bruch{6}{12} + \bruch{9}{12} +\bruch{8}{12} = \bruch{6 + 9 + 8}{12} = \bruch{23}{12} = 1 \bruch{11}{12}$

Dabei nennt man den kleinsten gemeinsamen Nenner, auf den sich die Brüche erweitern lassen, den Hauptnenner.

Zwei Brüche heißen gleichnamig, wenn sie denselben Nenner haben.

$}\bruch{3}{5}-\bruch{1}{4} = \bruch{12}{20}-\bruch{5}{20} = \bruch{12 - 5}{20}= \bruch{7}{20}$

Multiplikation von Brüchen

Zwei Brüche werden miteinander multipliziert,
indem man das Produkt der Zähler durch das Produkt der Nenner dividiert:

$\bruch{\mbox{Zähler} \cdot{} \mbox{Zähler}}{\mbox{Nenner}\cdot{}\mbox{Nenner}}$

$\bruch{7}{8} \cdot{} \bruch{4}{3} = \bruch{7\cdot{}4}{8\cdot{}3} = \bruch{7\cdot{}1}{2\cdot{}3} = \bruch{7}{6} = 1\bruch{1}{6}$

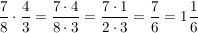
Division von Brüchen

Eine Zahl (auch ein Bruch) wird durch einen Bruch dividiert,
indem man mit dem Kehrbruch multipliziert:

$\bruch{77}{18} : \bruch{35}{27} = \bruch{77}{18} \cdot{} \bruch{27}{35} = \bruch{77 \cdot{} 27}{18 \cdot{} 35} = \bruch{11 \cdot{} 3}{2 \cdot{} 5} = \bruch{33}{10} = 3\bruch{3}{10}$

Merke: Vor dem Rechnen wird immer gekürzt!

Man kann auch Brüche durcheinander dividieren (Doppelbruch):

$\bruch{\bruch{4}{3} }{\bruch{8}{9} } = \bruch{4}{3} : \bruch{8}{9} = \bruch{4}{3} \cdot{} \bruch{9}{8} = \bruch{4 \cdot{} 9}{3 \cdot{} 8} = \bruch{3}{2} = 1\bruch{1}{2}$

Letzte Änderung: Mi 09.02.2005 um 15:59 von informix

Artikel • Seite bearbeiten • Versionen/Autoren • Titel ändern • Artikel löschen • Quelltext