Bernoulli-UngleichungSatz Bernoulli-Ungleichung
Voraussetzungen und Behauptung
Seien 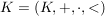 ein geordneter Körper und ein geordneter Körper und 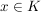 , , 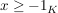 sowie sowie 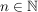 . .
Dann gilt (mit 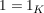 ): ):
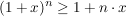 . .
Bemerkungen.
Beispiele.
Wir wählen jeweils ein 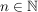 . Da . Da 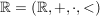 ein geordneter Körper ist, können wir obige Ungleichung dann für ein paar ein geordneter Körper ist, können wir obige Ungleichung dann für ein paar  -Werte aus -Werte aus 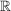 testen. testen.
1.) 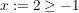 und und 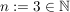 erfüllen die Voraussetzungen und liefern beim Einsetzen in die obige Ungkleichung: erfüllen die Voraussetzungen und liefern beim Einsetzen in die obige Ungkleichung:
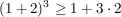
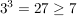
Da die letzte Ungleichung wahr ist, ist also auch die obere wahr.
2.) 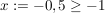 und und 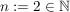 erfüllen die Voraussetzungen und liefern beim Einsetzen in die obige Ungkleichung: erfüllen die Voraussetzungen und liefern beim Einsetzen in die obige Ungkleichung:
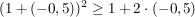
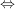
Da die letzte Ungleichung wahr ist, ist also auch die obere wahr.
3.) 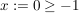 und und 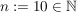 erfüllen die Voraussetzungen und liefern beim Einsetzen in die obige Ungkleichung: erfüllen die Voraussetzungen und liefern beim Einsetzen in die obige Ungkleichung:
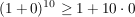
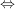
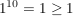 . .
Da die letzte Ungleichung wahr ist, ist also auch die obere wahr.
4.) 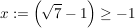 und und 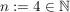 erfüllen die Voraussetzungen und liefern beim Einsetzen in die obige Ungkleichung: erfüllen die Voraussetzungen und liefern beim Einsetzen in die obige Ungkleichung:
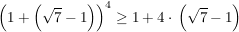
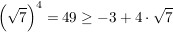 . .
Auch hier ist die letzte Ungleichung wahr (und damit auch die obere), denn:
Es gilt: 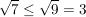 und daher folgt: und daher folgt:
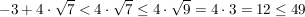
Beweis.
Per Induktion:
Induktionsanfang:
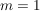 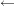 klar klar
Induktionsschritt:
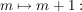
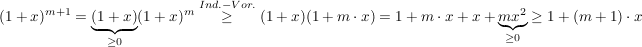 
| 