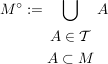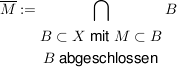TopologieDefinition Topologie
Universität
1.) Sei 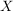 eine Menge. Ein Mengensystem eine Menge. Ein Mengensystem 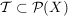 heißt Topologie (auf heißt Topologie (auf 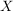 ) genau dann, wenn die folgenden Bedingungen ) genau dann, wenn die folgenden Bedingungen 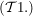 bis bis 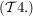 erfüllt sind: erfüllt sind:
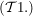 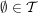
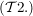 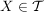
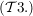 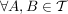 gilt: gilt: 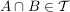 (d.h. (d.h. 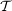 ist durchschnittsstabil!) ist durchschnittsstabil!)
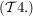 Ist Ist 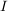 irgendeine Indexmenge und sind irgendeine Indexmenge und sind 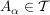 ( (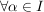 ) so gilt: ) so gilt:
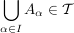 (d.h., (d.h., 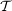 ist stabil unter Vereinigungen). ist stabil unter Vereinigungen).
Das Paar 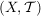 heißt dann topologischer Raum. Die Mengen heißt dann topologischer Raum. Die Mengen 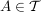 heißen offen (bzgl. heißen offen (bzgl. 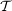 oder in oder in 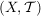 ). ). 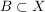 heißt abgeschlossen (bzgl. heißt abgeschlossen (bzgl. 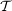 oder in oder in 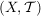 ) genau dann, wenn ) genau dann, wenn 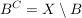 offen ist (d.h., falls offen ist (d.h., falls 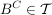 gilt). gilt).
2.) Sei 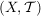 ein topologischer Raum. Ist ein topologischer Raum. Ist 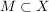 , so heißt , so heißt
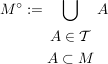
offener Kern oder Inneres von 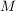 . .
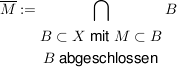
heißt Abschluß oder abgeschlossene Hülle von 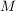 (ggf. schreibt man (ggf. schreibt man 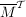 oder oder 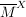 oder oder 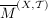 ). ).
3.) Sei 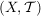 ein topologischer Raum und sei ein topologischer Raum und sei 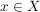 . Eine Menge . Eine Menge 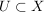 heißt Umgebung von heißt Umgebung von  genau dann, wenn es genau dann, wenn es 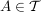 gibt mit gibt mit 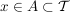 . Weiter heißt . Weiter heißt
 Umgebungsfilter. Umgebungsfilter.
|