idealeDie ideale Gasgleichung beschreibt den mathematischen Zusammenhang zwischen dem Druck p, dem Volumen V, der Stoffmenge (des Gases) n und der Temperatur T. Proportionalitaetsfaktor ist dabei die ideale Gaskonstante 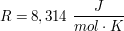 . .
pV=nRT
Der Gleichung liegen mehrere Naehrungen zu Grunde. So wird Beispielsweise angenommen, dass die Gasteilchen selbst kein Eigenvolumen aufweisen. Ausserdem wird davon ausgegangen, dass zwischen den Teilchen keine Wechselwirkungen stattfinden. Die van der Waals Gleichung beruecksichtigt diese Faktoren, ist jedoch deutlich komplexer.
Die Abweichungen von den realen Beobachtungen bei gemaessigten Temperaturen und Druecken sind vernachlaessigbar. Bei extremen Temperaturen oder Druecken hingegen koennen die Abweichungen enorm anwachsen.
Uebungsaufaben folgen...
1. a.) Welches Volumen nimmt ein Mol Wasserstoff bei einem Druck von 1 bar und einer Temperatur von 273 K ein?
b.) Welches Volumen nimmt Kohlenstoffdioxid unter den selben Bedingungen ein?
Zur Loesung der Aufgabe wird lediglich die ideale Gasgleichung nach V umgestellt.
Der Wasserstoff nimmt somit ein Volumen von rund 22,70 L ein.
Die Gleiche Stoffmenge an Kohlenstoffdioxid nimmt das selbe Volumen ein, da die ideale Gasgleichung nicht zwischen der Art der Teilchen, sondern lediglich der Menge unterscheidet.
| 