binomische FormelUnter einem Binom versteht man einen zweigliedrigen Summenterm der Form:
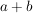 ; ; 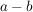
In der Mathematik kommen drei Arten von Produkten von Binomen häufig vor:
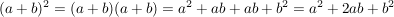
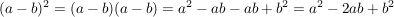
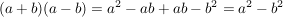
Beim Rechnen ist es von Vorteil die Endergebnisse auswendig zu wissen.
Dies ist besonders dann notwendig, wenn man einen Summenterm in ein Produkt umformen soll.
Dieses so genannte Faktorisieren spielt beim Lösen von Gleichungen und beim Kürzen von Bruchtermen eine sehr wichtige Rolle:
Regel:
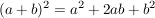 ("Plusregel") ... 1. Binomische Formel ("Plusregel") ... 1. Binomische Formel
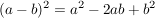 ("Minusregel") ... 2. Binomische Formel ("Minusregel") ... 2. Binomische Formel
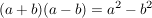 ("Plus-Minus-Regel") ... 3. Binomische Formel ("Plus-Minus-Regel") ... 3. Binomische Formel
| 