SchrankeZahlenfolgen oder Funktionen, deren Werte nicht ins Unendliche reichen, nennt man beschränkt.
Um die Beschränktheit konkret zu erfassen, verwendet man die Begriffe der oberen und der
unteren Schranke einer Zahlenfolge oder Funktion.
Zahlenfolgen:
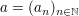 sei eine Zahlenfolge und sei eine Zahlenfolge und 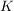 eine reelle Zahl. eine reelle Zahl.
Dann heisst 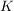 eine eine
obere Schranke der Zahlenfolge  , falls , falls 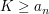 für alle für alle 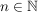
bzw. eine
untere Schranke der Zahlenfolge  , falls , falls 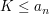 für alle für alle 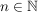
Funktionen:
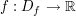 sei eine reelle Funktion und sei eine reelle Funktion und 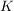 eine reelle Zahl. eine reelle Zahl.
Dann heisst 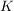 eine eine
obere Schranke der Funktion 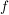 , falls , falls 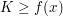 für alle für alle 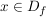
bzw. eine
untere Schranke der Funktion 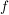 , falls , falls 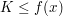 für alle für alle 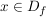
(Die Definitionen für den Fall der Zahlenfolgen sind Spezialfälle derjenigen für Funktionen,
denn eine Zahlenfolge ist eigentlich nichts anderes als eine Funktion mit Definitionsbereich 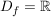 .) .)
Begriffe:
Besitzt eine Funktion oder eine Zahlenfolge eine obere Schranke, so heisst sie "nach oben beschränkt".
Besitzt sie eine untere Schranke, so heisst sie "nach unten beschränkt".
Liegt sowohl eine obere als auch eine untere Schranke vor, dann ist die Funktion bzw. die Folge "beschränkt".
Anwendung:
In der Grundlegung der Analysis (Analysis infinitorum, in etwa "Untersuchung des Unendlichen und des
unendlich Kleinen") spielt der Begriff Beschränktheit eine wichtige Rolle, dann man kann "das Unendliche
nur bändigen, indem man vom Endlichen, Beschränkten ausgeht" und Gesetze der Logik anwendet.
Als Beispiel nur ein wichtiger Satz:
Jede monotone und beschränkte Zahlenfolge besitzt einen Grenzwert. Konvergenzkriterien
Beschränktheit bei Mengen:
Der Begriff "beschränkt" hat eigentlich seine Heimat gar nicht unbedingt bei den Funktionen und Zahlenfolgen,
sondern in der Mengenlehre, genauer im Gebiet der halbgeordneten oder geordneten Mengen, der metrischen
Räume etc. . Dazu nur dies als Zugangslink: Wikipedia: Beschränktheit
| 