ZylinderDefinition Zylinder
Schule
Rotiert ein Viereck ABCD um eine Seite als Drehachse, so entsteht ein gerader Kreiszylinder.
Die Gerade AD heißt Zylinderachse, die Seite BC, die während der Drehung den Zylindermantel M beschreibt, heißt Mantellinie m. Die Seiten AB und DC beschreiben die Grundflächen (Grund- und Deckfläche) des Zylinders.
Berechnung der Mantelfläche
... nach Aufschneiden längs einer Mantellinie und Ausbreiten in die Ebene als Rechteck, das den Umfang 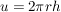 und die Höhe h als Seiten besitzt: und die Höhe h als Seiten besitzt:
Berechnung der Oberfläche
Addiert man die beiden Grundkreisflächen noch mit dem Inhalt  hinzu, ergibt sich die Oberfläche hinzu, ergibt sich die Oberfläche
Berechnung des Volumen
Universität
| 