ZentrumDefinition Zentrum
Universität
Es sei 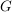 eine Gruppe. Man betrachte die Abbildung eine Gruppe. Man betrachte die Abbildung
![$ \Phi \, : \, \begin{array}{ccc} G & \to & Aut(G) \\[5pt] x & \mapsto & \varphi_x, \end{array} $ $ \Phi \, : \, \begin{array}{ccc} G & \to & Aut(G) \\[5pt] x & \mapsto & \varphi_x, \end{array} $](/teximg/2/2/00394222.png) , ,
wobei 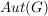 die Automorphismengruppe von die Automorphismengruppe von 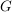 und und
![$ \varphi_x \, : \, \begin{array}{ccc} G & \to & G \\[5pt] b & \mapsto & xbx^{-1} \end{array} $ $ \varphi_x \, : \, \begin{array}{ccc} G & \to & G \\[5pt] b & \mapsto & xbx^{-1} \end{array} $](/teximg/3/2/00394223.png)
ein innerer Automorphismus sei.
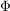 ist ein Gruppenhomomorphismus: ist ein Gruppenhomomorphismus:
Wegen
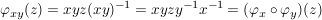
ist 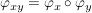 , d.h. , d.h.
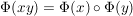 . .
Der Kern dieses Homomorphismus bestimmt sich zu
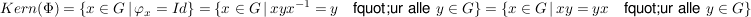 . .
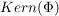 wird häufig mit wird häufig mit 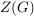 bezeichnet und heißt das Zentrum von bezeichnet und heißt das Zentrum von 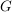 . .
Das Zentrum "misst" den "Grad der Kommutativität" von 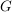 . Es ist . Es ist 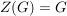 genau dann, wenn genau dann, wenn 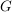 abelsch ist. Elemente abelsch ist. Elemente 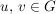 heißen vertauschbar, wenn heißen vertauschbar, wenn 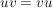 gilt. Das Zentrum besteht also aus all den Elementen von gilt. Das Zentrum besteht also aus all den Elementen von 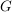 , die mit jedem Element von , die mit jedem Element von 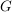 vertauschbar sind. vertauschbar sind.
Quelle: isbn3446130799
| 