RelationDefinition Relation (Zuordnung)
Schule
Eine Relation ordnet Elementen einer Menge 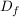 (Definitionsmenge) Elemente einer Menge (Definitionsmenge) Elemente einer Menge 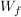 (Wertemenge) zu. (Wertemenge) zu.
Bemerkung
Bei einer Relation kommt es nicht darauf an, dass jedem Element der Definitionsmenge genau ein Element der Wertemenge zugeordnet ist, es können vielmehr auch mehr als eins sein.
Wird durch f genau ein Element eindeutig zugeordnet, dann spricht man von einer Funktion.
Beispiele für Relationen
Universität
Es seien X und Y zwei Mengen.
Eine Teilmenge 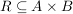 des kartesischen Produkts des kartesischen Produkts 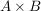 heißt Relation zwischen A und B. heißt Relation zwischen A und B.
Eine Teilmenge 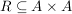 des kartesischen Produkts des kartesischen Produkts 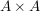 heißt Relation auf A. heißt Relation auf A.
Relationen mit speziellen Eigenschaften
reflexiv 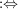 TODO TODO
transitiv 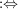 TODO TODO
symmetrisch 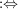 TODO TODO
linksvollständig 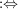 TODO TODO
rechtseindeutig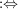 TODO TODO
Eine linksvollständige und rechtseindeutige Relation heißt Abbildung.
Beispiele für Relationen
TODO
| 