PrismaEin Prisma ist ein spezieller geometrischer Körper. Er entsteht durch Verschiebung einer Grundflächenfigur aus der Ebene heraus, einer sogenannten Parallelverschiebung.
Ist diese Verschiebung senkrecht zur Grundfläche, liegt die neue "Dachfläche" direkt über der Grundfläche, und man erhält ein sogenanntes Gerades Prisma, sonst spricht man von schiefen Prismen.
Ein Prisma besteht also aus der sogenannten Grundfläche G (Die von der Form der Grundfigur abhängig ist) und einer Mantelfläche M.
Das Volumen eines Prismas berechnet sich wie folgt:
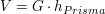
(Dies gilt für alle Prismen, ob gerade oder schief)
Bei geraden Prismen gilt für die Matelfläche M:
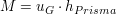
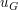 ist hierbei der Umfang der Grundfläche. ist hierbei der Umfang der Grundfläche.
Für die Oberfläche des gesamtem Prismas gilt dann:
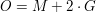
| 