KurvenflächenbestimmungWie bestimme ich die Fläche zwischen zwei Funktionsgraphen?
Seien die Funktionen 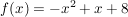 und und  gegeben. gegeben.
Dann bestimme man zunächst die Schnittpunkte der beiden Graphen:
Um die Fläche zwischen den beiden Graphen zu berechnen, berechnet man das bestimmte Integral der Differenz der beiden Funktionen:
Bemerkungen:
- Dabei kommt es nur auf die Schnittpunkte der Graphen an, nicht jedoch auf eventuell vorhandene Nullstellen.
- Die Betragsstriche sind notwendig, wenn man nicht genau weiß, welcher der beiden Graphen "oben" ist.
| 


