InversionInversion einer komplexen Zahl
Anwendungsfall: Der komplexe Widerstand 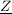 ist definiert als Kehrwert des Leitwertes ist definiert als Kehrwert des Leitwertes 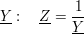
Den Vorgang der Kehrwertbildung einer komplexen Zahl z (bitte keine Verwechslung mit oben genanntem komplexen Widerstand 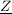 ) nennt man Inversion. ) nennt man Inversion.
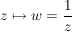
In der Exponentialform:
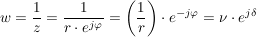
es ist also:
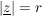
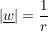
Beispiel:
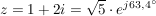
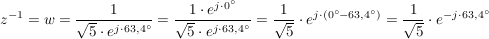
Da die reellen Zahlen eine Teilmenge der komplexen Zahlen sind, ist es leicht einzusehen, dass auch dort die Kehrwertbildung im gleichen Maße gilt.
z=3
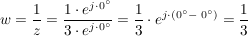
Übung:
z=3-4j
w=0,12+0,16j
Allgemein:
Es sei mit 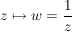 eine komplexe Funktion f(z) definiert, so werden die z-Werte in einer komplexen z-Ebene auf die w-Punkte einer komplexen w-Ebene abgebildet. eine komplexe Funktion f(z) definiert, so werden die z-Werte in einer komplexen z-Ebene auf die w-Punkte einer komplexen w-Ebene abgebildet.
Im Nullpunkt z=0 ist die Funktion nicht definiert (der zugehörige Punkt läge im Unendlichen!)
Inversionsregeln:
z-Ebene 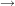 w-Ebene w-Ebene
1. Gerade (durch den Nullpunkt)  Gerade (durch den Nullpunkt) Gerade (durch den Nullpunkt)
2. Gerade (nicht durch den Nullpunkt)  Kreis (durch den Nullpunkt) Kreis (durch den Nullpunkt)
3. Mittelpunktskreis  Mittelpunktskreis Mittelpunktskreis
4. Kreis (durch den Nullpunkt)  Gerade (nicht durch den Nullpunkt) Gerade (nicht durch den Nullpunkt)
5. Kreis (nicht durch den Nullpunkt)  Gerade (durch den Nullpunkt) Gerade (durch den Nullpunkt)
Beispiel:
Inversion einer Widerstandsortskurve des Reihenschwingkreises R-L-C
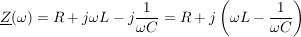
Diese Gerade verläuft, da R=c=const und 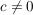 als Parallele zur j-Achse; es ist also eine Gerade nach Inversionsregel 2! als Parallele zur j-Achse; es ist also eine Gerade nach Inversionsregel 2!
Inversion:
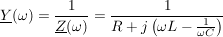
Nun gilt es den kleinsten Abstand zum Nullpunkt zu ermitteln: es ist natürlich der Schnittpunkt mit der reellen Achse (eine kleine Skizze verdeutlicht es sofort).
Dafür muss jedoch der imaginäre Anteil identisch verschwinden, d.h.
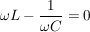
oder
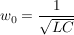
Dann ist aber:
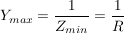 der Durchmesser des gesuchten Kreises und wenn man das noch weiter verfolgt, dann muss natürlich auch der Kreis durch den Ursprung gehen, denn der Mittelpunkt liegt ja automatisch auf der Hälfte des Durchmessers ebenfalls auf der reellen Achse. der Durchmesser des gesuchten Kreises und wenn man das noch weiter verfolgt, dann muss natürlich auch der Kreis durch den Ursprung gehen, denn der Mittelpunkt liegt ja automatisch auf der Hälfte des Durchmessers ebenfalls auf der reellen Achse.
Übung:
Man bilde aus der Parallelschaltung R||L mit R,L=const und 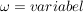 die Ortskurve des komplexen Leitwertes. die Ortskurve des komplexen Leitwertes.
Es ist zu beachten, dass sich in einer Parallelschaltung die komplexen Leitwerte addieren.
Viel Erfolg
| 