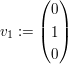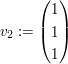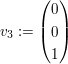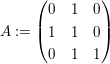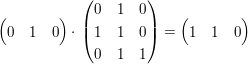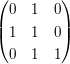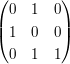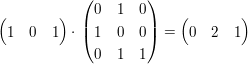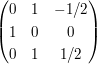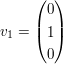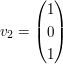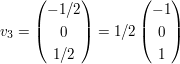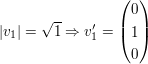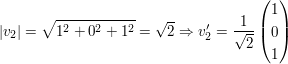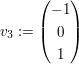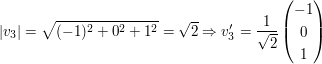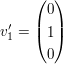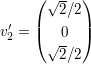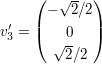GramSchmidtGram Schmidt
Beschreibung
Das Gram-Schmidt-Verfahren dient dazu, eine Orthonormale Basis eines Vektorraums zu berechnen. Man möchte erreichen, dass die Basisvektoren paarweise senkrecht aufeinander stehen (also dass die Basisvektoren im Skalarprodukt mit den anderen 0 ergeben), und dass sie die Länge 1 haben, also normiert sind.
Algorithmus 1 (standard)
Das Verfahren unterteilt man in zwei Schritte:
1) Orthogonalisierung
2) Normalisierung
1) Orthogonalisierung
Man nehme sich den ersten Basisvektor  , und halte diesen fest. , und halte diesen fest.
Dann nehme man sich der Reihe nach den zweiten, dritten, i.ten Basisvektor, und berechne 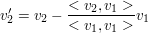
Dann nehme man sich den dritten Basisvektor und berechne 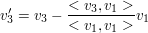
Das führe man allgemein fort, man berechne also für alle i von 2 bis #Basisvektoren 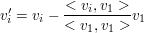
Nun hat man erreicht, dass die Basisvektoren 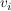 , i=2,...,#Basisvektoren senkrecht auf dem ersten Basisvektor stehen. , i=2,...,#Basisvektoren senkrecht auf dem ersten Basisvektor stehen.
Als nächstes ist zu erreichen, dass der die restlichen Basisvektoren 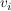 , i=3,...,#Basisvektoren senkrecht auf dem zweiten stehen. , i=3,...,#Basisvektoren senkrecht auf dem zweiten stehen.
Dazu ist der obige Algorithmus mit den neuen Basisvektoren weiter zu verwenden, allerdings sehen die Indizes nun so aus:
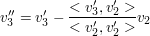 , allgemein: , allgemein:
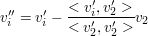
Wenn man so alle weiteren Basisvektoren orthogonalisiert hat, wiederhole man diesen Schritt nocheinmal, denn nun muss man erreichen, dass der vierte, fünfte usw. Basisvektor auf dem dritten senkrecht steht.
Dies ist das Standardverfahren. Es gibt allerdings einen schöneren Algorithmus:
Algorithmus 2
Dieser Algorithmus ist im wesentlichen der oben vorgestellte Algorithmus, aber er verläuft viel einheitlicher und schneller und m.E. auch sicherer ab.
Diesen Algorithmus möchte ich anhand eines Beispieles zeigen, da es so deutlich leichter ist, ihn zu verstehen:
Gegeben seien die Basisvektoren 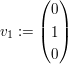 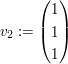 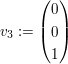
Nun fassen wir die drei Basisvektoren zu einer Matrix zusammen:
Sei 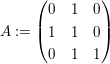
Nun berechnen wir 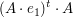 , also berechnen wir das Produkt aus dem Transponierten der ersten Spalte der Matrix mit der Matrix selbst: , also berechnen wir das Produkt aus dem Transponierten der ersten Spalte der Matrix mit der Matrix selbst:
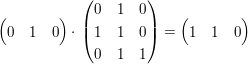
Dies kann man auch als Skalarprodukt der ersten Spalte mit allen drei Spalten verstehen.
Nun schreiben wir den eben berechneten Vektor unter die Matrix, und versuchen, durch elementare Spaltentransformationen Nullen in dem eben erzeugten Vektor zu erzeugen:
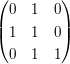
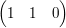
Man versucht nun, in der zweiten Spalte in der unteren Matrix eine 0 zu erzeugen. Das geht, indem man das -1 fach der ersten Spalte zur zweiten Spalte addiert. Die Matrix schaut dann so aus:
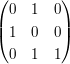
Nun berechnet man wieder einen ähnlichen Zeilenvektor wie oben, nur, dass man diesmal die transponierte zweite Spalte der Matrix mit obigen, neuen Matrix multipliziert:
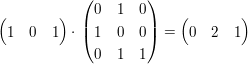
Die erste Null in dem Zeilenvektor muss dort stehen, denn das zeigt ja gerade an, dass die ersten beiden Vektoren senkrecht aufeinander stehen. Das ist ja auch unser Ziel.
Nun nehmen wir uns wieder den obigen Zeilenvektor, und schreiben ihn unter unsere Matrix:
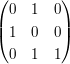
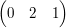
Nun versuchen wir, in der letzen Spalte in dem Zielenvektor eine "0" zu erzeugen. Dazu addieren wir das -1/2-fache der zweiten Zeile zur dritten. Dann schaut die neue Matrix so aus:
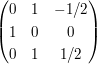
Berechnet man nun die Skalarprodukte jedes Vektors mit dem anderen, so wird man feststellen, dass alle Skalarprodukte 0 sind. So ist dieser Algorithmus auch konstruiert. Dies zeigt uns an, dass nun die Basisvektoren paarweise senkrecht aufeinander stehen.
Hinweis: Sollte es mehr als drei Basisvektoren geben, so fahre man dann mit dem obigen Algorithmus fort, indem man den transponierten dritten Spaltenvektor der neuen Matrix mit der Matrix multipliziert, und das verfahren wiederholt, so lange, bis man an der letzten Spalte angekommen ist.
Nun hat man eine Orthogonalbasis erzeugt. Es fehlt noch, dass die Basisvektoren normiert sind. Das ist aber sehr einfach:
Gegeben sind nun die orthogonalen Basisvektoren
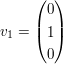 , , 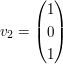 , , 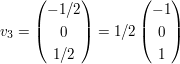
Nun berechne man die Beträge der Vektoren, und teile dann die Vektoren durch diese, so dass die Basisvektorn die normierte Länge 1 haben.
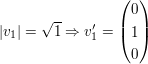
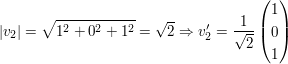
Hinweis zum dritten Basisvektor: Man zieht in der Regel Skalare aus dem Vektor heraus, so dass man im Vektor dann nur noch ganzzahlige Werte stehen hat. Da es sich hier um Basisvektoren handelt, wo nur die Richtung entscheidend ist, lässt man dann diese Skalare im weiteren einfach weg:
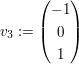
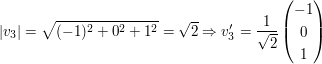
Also hat man die drei Basisvektoren orthonormalisiert, die nun so aussehen:
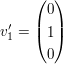
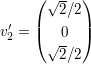
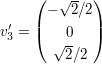
Ausblick
Nun hat man eine Orthonormale Basis gefunden. Steckt man diese Vektoren wieder in eine Matrix, so erhält man eine Orthonormale Matrix, für die gilt: 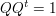 , 1 ist die Einheitsmatrix. , 1 ist die Einheitsmatrix.
Mit dieser Information kann man wunderbar die QR-Faktorisierung durchführen, denn A=QR, Q hat man gegeben durch die Matrix oben, und es gilt dann: 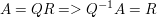 und mit dem Wissen, dass und mit dem Wissen, dass 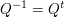 lässt sich sehr einfach R berechnen, wobei R eine obere Dreiecksmatrix ist. lässt sich sehr einfach R berechnen, wobei R eine obere Dreiecksmatrix ist.
|