ErgänzungDefinition Quadratische Ergänzung
Eine Quadratische Ergänzung nennt man die Erweiterung eines Terms der Form
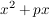
zu einer binomischen Formel:

Die quadratische Ergänzung wird häufig zum Lösen quadratischer Gleichungen oder zur Scheitelpunktsbestimmung von Parabeln benutzt.
Beispiel
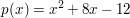 ist der Term einer Parabel. ist der Term einer Parabel.
Der Scheitelpunkt der Parabel soll bestimmt werden.
Das geschieht mit der Methode der quadratischen Ergänzung:
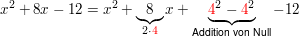
geschicktes Setzen von Klammern erlaubt es, einen binomischen Term zu sehen:
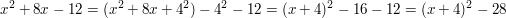
Diese Methode wird vor allem bei der Bestimmung der Scheitelpunktform einer Parabel angewandt.
siehe auch: p/q-Formel
| 
