EbenengleichungenGegenseitige Lage zweier Ebenen im Raum
Für die gegenseitige Lage zweier Ebenen
und
gibt es drei Möglichkeiten:
- die Ebenen fallen zusammen (sind also identisch, werden aber durch zwei unterschiedliche Gleichungen beschrieben),
- die Ebenen sind echt parallel (haben also keinen Punkt gemeinsam),
- die Ebenen schneiden sich in einer Geraden.
Die Ebenengleichungen können stets durch Division auf eine Form gebracht werden, in der die Koeffizienten r_i bzw. s_i (i=1,2,3) teilerfremde ganze Zahlen sind.
(1) Gilt nach einer solchen Umformung: 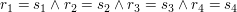 , ,
dann fallen die Ebenen zusammen, die Gleichungen beschreiben in Wahrheit dieselbe Ebene:  . .
(2) Gilt nach einer solchen Umformung:  , ,
dann sind die beiden Ebenen echt parallel, sie haben keinen gemeinsamen Punkt:  . .
(3) Stimmen die Koeffizienten  nicht paarweise überein, nicht paarweise überein,
dann schneiden sich die Ebenen in einer Schnittgeraden s.
Die Schnittgerade einer Ebene mit einer Koordinatenebene heißt Spurgerade.
Vorgehen beim Überprüfen
Sind die beiden Ebenen durch die Normalenform oder die Koordinatenform der Ebenengleichung gegeben, kann man nach dem oben genannten Schema die Lage überprüfen:
(1)  und und 
(2)  und und 
(3) Man betrachtet z.B. das lineare Gleichungssystem:
Da die zwei Gleichungen drei Variable enthalten, kann eine frei gewählt werden und anschließend die anderen bestimmt werden:
siehe: ![Link auf "http://de.wikipedia.org/wiki/Schnittgerade#Zur_Lage_von_Ebenen" [link]](/images/popup.gif) Wikipedia Wikipedia
| 

