Binomialkoeffizient Erklärung

1. Anwendung

Angenommen, du möchtest aus einer Gruppe von n Menschen eine kleinere Gruppe mit k Menschen zusammenstellen, zum Beispiel aus den 30 (=n) Schülern einer Klasse eine Fußballmannschaft von 11 (=k) Spielern.
Dann gibt der Binomialkoeffizient an, wie wiele verschiedene Fußballmannschaften du bilden kannst.
Ein bisschen formaler: Ich nummeriere die Schüler der Einfachheit halber mit . Dann wäre eine mögliche Fußballmannschaft:

1. Möglichkeit:
2. Möglichkeit:
3. Möglichkeit:

. Möglichkeit:

Diese Liste von Fußballmannschaften ist also Fußballmannschaften lang.

2. Anwendung

Ein bißchen abstrakter kann man also die Binomialkoeffizienten dazu benutzen, die Anzahl der k-elementigen Teilmengen einer n-elementigen Menge zu bestimmen.
Die Menge hat also Teilmengen, die 11 Elemente enthalten.

3. Berechnung

Die Formel zur Berechnung des Binomialkoeffizienten hast du ja bereits mitgeliefert, du scheinst aber noch nicht so richtig damit umgehen zu können. Also, die Formel lautet ja

Dabei bedeutet die Fakultät von n, genauer: . Zum Beispiel ist .

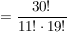
Für das Beispiel oben würdest du also rechnen:

(denn: )

(kürzen!)

4. Beweis

Stelle dir die n-elementige Menge vor, aus der wir jetzt eine k-elementige Teilmenge bilden wollen (falls dir das zu abstrakt ist, stelle dir die Schüler und die Fußballmanschaft vor und für n und k feste Zahlen, beispielsweise n=30 und k=11).

Nun stelle ich Element für Element die Teilmenge zusammen, indem ich nacheinander die k Plätze der Teilmenge belege:

Zu Beginn sind alle Plätze unbelegt.

Nun wähle ich aus der Menge N das erste Element aus; da die Menge N zu diesem Zeitpunkt aus n Elementen besteht, habe ich n verschiedene Möglichkeiten, den ersten Platz zu belegen.

1. Platz: , erster Platz belegt (gekennzeichnet einfach mit X)

Für die Belegung des zweiten Platzes kann ich nur noch aus n-1 Elementen wählen.

2. Platz:

Für die Belegung des dritten Platzes kann ich nur noch aus n-2 Elementen wählen.

3. Platz:

Für die Belegung des vorletzten Platzes kann ich noch aus n-k+2 Elementen wählen.

(k-1). Platz:

Für die Belegung des letzten Platzes kann ich noch aus n-k+1 Elementen wählen.

k. Platz: , alle Plätze belegt.

Insgesamt gibt es also Möglichkeiten, diese k Plätze zu belegen (zur Verdeutlichung noch mal das Beispiel mit der Fußballmannschaft: Wir haben da ja n=30 und k=11, also Möglichkeiten).

Dieses Produkt kann man auch mit Hilfe von Fakultäten ausdrücken:

im Zähler steht nun gerade n!:

So, jetzt müssen wir nur noch eine Korrektur vornehmen, denn: Auf diese Art und Weise der Teilmengenbildung erhalten wir mehrfach dieselbe Teilmenge, ich behaupte (und zeige gleich), dass wir so jede Teilmenge k!-mal erhalten.

Zum Beispiel wird (1,2,3,4,5,6,7,8,9,10,11) und (2,1,3,4,5,6,7,8,9,10,11) getrennt gezählt, es werden also solche Auswahlen mehrfach gezählt, die sich nur durch die Reihenfolge der Elemente unterscheiden (in der obigen Darstellung habe ich auch bewußt keine Mengenklammern gewählt, sondern runde Klammern. Mathematisch heißt ein Tupel; dies ist eine Liste von Elementen, bei der es auf die Reihenfolge ankomm, im Unterschied zu Mengen übrigens, denn: , aber , aber das nur nebenbei ;-)).

In wie viele verschiedene Reihenfolgen kann man denn k Elemente bringen?
Führe hier wieder ein Gedankenexperiment durch (dasselbe wie oben übrigens) und wähle aus einer k-elementigen Menge (diesmal) k Elemente aus; du hast

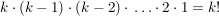
Möglichkeiten dazu.

Jede Teilmenge wurde also bei unserem Versuch oben k!-fach gezählt, wir müssen also unser Zwischenergebnis noch durch k! teilen: