Benutzer:tobit09/Beweis-Tutorial A17Beweis-Tutorial
 4. "für alle"-Aussagen 4. "für alle"-Aussagen
Lösungsvorschlag Aufgabe 17
Aufgabe:
Sei 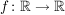 eine gerade Funktion. Zeige, dass dann auch die Funktion eine gerade Funktion. Zeige, dass dann auch die Funktion  gerade ist. gerade ist.
Überlegungen zur Lösung:
Gegeben:
eine Funktion 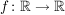
 gerade, d.h. gerade, d.h. 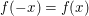 für alle reellen Zahlen für alle reellen Zahlen  . .
die Funktion 
Zu zeigen:
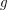 gerade, d.h. gerade, d.h.  für alle reellen Zahlen für alle reellen Zahlen 
Wir betrachten also eine beliebig vorgegebene reelle Zahl 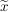 und wollen und wollen 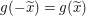 zeigen. zeigen.
Es gilt 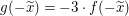 und und 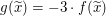 ; also ist ; also ist 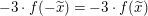 zu zeigen. zu zeigen.
Bringen wir nun die gegebene Aussage, dass 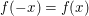 für alle reellen Zahlen für alle reellen Zahlen  gilt, ins Spiel: Da gilt, ins Spiel: Da 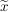 eine reelle Zahl ist, gilt somit insbesondere eine reelle Zahl ist, gilt somit insbesondere 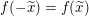 . .
Also wie gewünscht 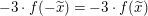 . .
Lösungsvorschlag:
Sei 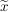 eine beliebig vorgegebene reelle Zahl. eine beliebig vorgegebene reelle Zahl.
Da  gerade ist, gilt gerade ist, gilt 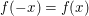 für alle reellen Zahlen für alle reellen Zahlen  . .
Insbesondere gilt dies für unsere reelle Zahl 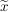 , also , also 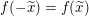 . .
Es folgt  . .
Da 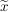 beliebig vorgegeben war, gilt somit beliebig vorgegeben war, gilt somit  für alle reellen Zahlen für alle reellen Zahlen  . .
Also ist 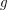 gerade. gerade.
| 