Kursdaten anzeigen • Liste aller Vorkurse • Druckansicht
Dipl. math. Felix Fontein
Dipl. math. Dieter Osterholz | www.matheraum.de
Algebra-Training 2006
Aufgabenblatt 5
Abgabe: Fr 13.10.2006 12:00 | 06.10.2006 | | In diesen Aufgaben geht es darum, denn bisher gelernten Stoff zu wiederholen und 'praktisch' anzuwenden. | | Aufgabe 18 | Für eine endliche Gruppe G sei p der kleinste Primteiler der Gruppenordnung und H eine Untergruppe vom Index p. Zeige: H ist Normalteiler in G.
(aus Lang, Algebra)
| | Aufgabe 19 | Konstruiere alle Gruppen der Ordung 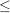 5. 5.
| | Aufgabe 20 | | Konstruiere mind. eine und höchstens zwei nicht-kommutative Gruppen der Ordnung 8.
| | Aufgabe 21 | Die 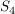 ist (abstrakt) die Gruppe der Permutationen von 4 Elementen oder auch der bijektiven Abbildungen einer 4elementigen Menge auf sich. Konkret werden als Elemente meistens die Zahlen von 1 bis 4 genommen. ist (abstrakt) die Gruppe der Permutationen von 4 Elementen oder auch der bijektiven Abbildungen einer 4elementigen Menge auf sich. Konkret werden als Elemente meistens die Zahlen von 1 bis 4 genommen.
Die Schreibweise für eine Permutation  ist dann z. B. ist dann z. B.
 = = 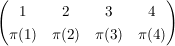
Man beachte: Permutationen sind Abbildungen, die Verknüpfung wird dann nach heute üblicher Konvention von rechts nach links gelesen, also 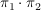 bedeutet 'erst bedeutet 'erst  dann dann 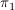 '. '.
Man bestimme die Untergruppen, die Normalteiler und das Zentrum. |
Kursdaten anzeigen • Liste aller Vorkurse • Druckansicht
|
