Kursdaten anzeigen • Liste aller Vorkurse • Druckansicht
Dietlind Bäro
Daniel Metzsch | www.matheraum.de
Mathe für's ABI 2008
Aufgabenblatt 3
Abgabe: So 25.11.2007 11:00 | 11.11.2007 | | Nur mit grafikfähigem Taschenrechner oder CAS. | | Aufgabe 1 | (mit CAS oder grafikfähigem Taschenrechner)
Gegeben ist eine Funktionenschar 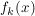 mit: mit: 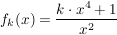 und und 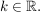
a) Berechnen Sie die Nullstellen und die relativen Extrempunkte der Funktionenschar 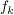 und begründen Sie, dass keiner der Graphen die x-Achse schneidet, wenn er einen relativen Extrempunkt besitzt. und begründen Sie, dass keiner der Graphen die x-Achse schneidet, wenn er einen relativen Extrempunkt besitzt.
b) Ermitteln Sie die Ortskurve aller Extrempunkte
c) Ordnen Sie den Funktionsgraphen von 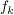 begründet ihre Funktionsgleichung zu. begründet ihre Funktionsgleichung zu.
![[Dateianhang]](uploads/forum/00323516/forum-i00323516-n001.png)
d) Gegeben sind die Funktionen: 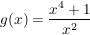 und und 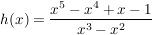
Stellen Sie für h einen Bezug zur Funktionenschar her und erläutern Sie begründet, wodurch sich die Graphen von g und h unterscheiden. |
Kursdaten anzeigen • Liste aller Vorkurse • Druckansicht
|

![[Dateianhang]](uploads/forum/00323516/forum-i00323516-n001.png)