Kursdaten anzeigen • Liste aller Vorkurse • Druckansicht
Dipl. math. Felix Fontein
Dipl. math. Dieter Osterholz | www.matheraum.de
Algebra-Training 2006
Aufgabenblatt 4
Abgabe: Fr 06.10.2006 12:00 | 22.09.2006 | | Wie angekuendigt springen wir erstmal fuer den Abschnitt 5.1 nach Kapitel 5. | | Aufgabe 14 |
Sei 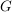 eine Gruppe, eine Gruppe, 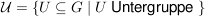 die Menge aller Untergruppen von die Menge aller Untergruppen von 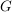 und und 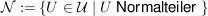 die Menge aller Normalteiler in die Menge aller Normalteiler in 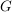 . .
(i) Zeige, dass 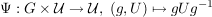 eine Operation von eine Operation von 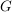 auf auf 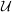 liefert. liefert.
(ii) Zeige, dass die Bahn eines Elementes 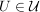 genau dann aus einem Element besteht, wenn genau dann aus einem Element besteht, wenn 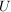 ein Normalteiler in ein Normalteiler in 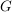 ist. ist.
(iii) Sei 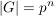 fuer eine Primzahl fuer eine Primzahl 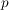 und und 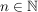 . Dann ist . Dann ist 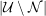 durch durch 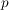 teilbar. teilbar.
| | Aufgabe 15 |
Sei 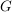 eine endliche Gruppe, eine endliche Gruppe, 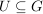 eine Untergruppe und eine Untergruppe und 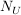 der Normalisator von der Normalisator von 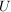 in in 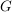 . Setze . Setze 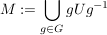 . .
(i) Beweise  . .
(ii) Sei 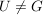 . Zeige, dass dann auch . Zeige, dass dann auch  ist. ist.
| | Aufgabe 16 |
Sei 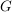 eine Gruppe, eine Gruppe, 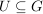 eine Untergruppe und eine Untergruppe und 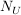 bzw. bzw. 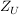 der Normalisator bzw. Zentralisator von der Normalisator bzw. Zentralisator von 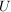 in in 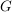 . Zeige, dass . Zeige, dass 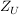 ein Normalteiler in ein Normalteiler in 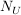 ist und dass ist und dass 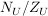 isomorph zu einer Untergruppe von der Automorphismengruppe isomorph zu einer Untergruppe von der Automorphismengruppe 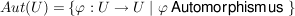 ist. ist.
| | Aufgabe 17 |
Sei 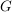 eine Gruppe mit eine Gruppe mit 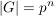 , wobei , wobei 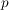 eine Primzahl sei und eine Primzahl sei und 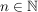 . Zeige, dass das Zentrum . Zeige, dass das Zentrum 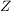 von von 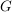 mindestens mindestens 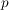 Elemente umfasst. Elemente umfasst.
Hinweis: Klassengleichung.
|
Kursdaten anzeigen • Liste aller Vorkurse • Druckansicht
|
