Kursdaten anzeigen • Liste aller Vorkurse • Druckansicht
Dipl. math. Felix Fontein
Dipl. math. Dieter Osterholz | www.matheraum.de
Algebra-Training 2006
Aufgabenblatt 6
Abgabe: Fr 10.07.2009 15:00 | 17.11.2006 | | Es werden insgesamt 6 Aufgaben. | | Aufgabe 1 | Man führe die in Satz 4 beschriebene Division mit Rest im Polynomring ![$ \IZ[X] $ $ \IZ[X] $](/teximg/0/3/00022630.png) in folgenden Fällen explizit durch: in folgenden Fällen explizit durch:
(i) f = 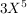 + + 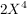 - - 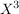 + + 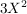 - 4X + 7, g = - 4X + 7, g = 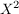 - 2X + 1 - 2X + 1
(ii) f = 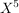 + +  - - 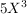 + +  + 2X -1, g = + 2X -1, g = 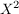 - 1 - 1
| | Aufgabe 2 | Sei K ein Körper und g 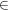 K[X] ein Polynom einer Variablen vom Grad d > 0. Man beweise die Existenz der sogenannten g-adischen Entwicklung: Zu f K[X] ein Polynom einer Variablen vom Grad d > 0. Man beweise die Existenz der sogenannten g-adischen Entwicklung: Zu f 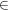 K[X] gibt es eindeutig bestimmte Polynome K[X] gibt es eindeutig bestimmte Polynome 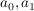 ... ... 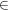 K[X] vom Grad < d, K[X] vom Grad < d, 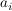 = 0 für fast alle i, mit f = = 0 für fast alle i, mit f = 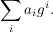
| | Aufgabe 3 | Es sei R ein Ring, der ein nilpotentes Element a 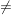 0 enthalte; nilpotent bedeutet, daß es ein n 0 enthalte; nilpotent bedeutet, daß es ein n 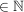 mit mit  = 0 gibt. Man zeige, daß die Einheitengruppe R* eine echte Untergruppe der Einheitengruppe (R[X])* ist. = 0 gibt. Man zeige, daß die Einheitengruppe R* eine echte Untergruppe der Einheitengruppe (R[X])* ist.
| | Aufgabe 4 | Man bestimme den kleinsten Unterring von 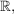 welcher welcher 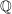 und und 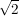 enthält, und zeige, daß dieser bereits ein Körper ist. enthält, und zeige, daß dieser bereits ein Körper ist.
|
Kursdaten anzeigen • Liste aller Vorkurse • Druckansicht
|
