Kursdaten anzeigen • Liste aller Vorkurse • Druckansicht
| www.matheraum.de
Mathematik des 11. Jahrgangs
Aufgabenblatt 1
Abgabe: Sa 30.11.2013 19:00 | 10.11.2013 | | Aufgabe 1 | Gegeben ist die ganzrationale Funktion 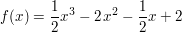 mit mit  . .
 Führen Sie eine vollständige Kurvendiskussion der Funktion Führen Sie eine vollständige Kurvendiskussion der Funktion 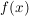 durch und zeichnen Sie den Graphen der Funktion im Intervall durch und zeichnen Sie den Graphen der Funktion im Intervall ![$ I = \left[-1,5\,; 4,5\right]\,. $ $ I = \left[-1,5\,; 4,5\right]\,. $](/teximg/1/2/01606721.png)
 Die Tangente an die mittlere Nullstelle der Funktion schließt mit den Koordinatenachsen ein rechtwinkliges Dreieck ein. Welchen Flächeninhalt hat dieses und wie lang ist seine Hypotenuse? Die Tangente an die mittlere Nullstelle der Funktion schließt mit den Koordinatenachsen ein rechtwinkliges Dreieck ein. Welchen Flächeninhalt hat dieses und wie lang ist seine Hypotenuse?
Viel Erfolg!
 Eine vollständige Kurvendiskussion ganzrationaler Funktionen beinhaltet: Eine vollständige Kurvendiskussion ganzrationaler Funktionen beinhaltet:
- Definitions- und Wertebereich,
- Nullstellen und Ordinatenabschnitt,
- Symmetrie- und Monotoniebetrachtungen (Monotonie wird häufig auch weggelassen),
- mindestens die ersten beiden Ableitungen,
- Extrema und Wendepunkte,
- Untersuchung des Verhaltens im Unendlichen
- graphische Darstellung der Funktion (und gern auch ihrer Ableitungen). | | Aufgabe 2 | Diskutieren Sie die Funktion 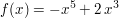 mit mit 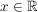 und zeichnen Sie den Graphen der Funktion im Intervall und zeichnen Sie den Graphen der Funktion im Intervall ![$ I = \left[-2\,; 2\right]\,. $ $ I = \left[-2\,; 2\right]\,. $](/teximg/2/5/01609652.png) Unter welchen Winkeln schneidet der Funktionsgraph die Koordindatenachsen? Unter welchen Winkeln schneidet der Funktionsgraph die Koordindatenachsen?
| | Aufgabe 3 | Gegeben sei die Funktionsschar  mit dem reellen Parameter mit dem reellen Parameter 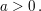
 Führen Sie eine vollständige Kurvendiskussion für Führen Sie eine vollständige Kurvendiskussion für 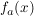 durch und zeichnen Sie den Graphen für den Parameter durch und zeichnen Sie den Graphen für den Parameter 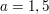 im Intervall im Intervall ![$ I=\left[-5\,;\,5\right] $ $ I=\left[-5\,;\,5\right] $](/teximg/0/4/02017240.png) . .
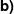 Für welchen Wert von Für welchen Wert von  geht die Wendenormale im rechten Wendepunkt durch den linken Hochpunkt? geht die Wendenormale im rechten Wendepunkt durch den linken Hochpunkt?
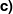 Für welchen Wert von Für welchen Wert von  stehen die Wendetangenten orthogonal aufeinander? stehen die Wendetangenten orthogonal aufeinander? |
Kursdaten anzeigen • Liste aller Vorkurse • Druckansicht
|
