MatheRaum - Offene Informations- und Nachhilfegemeinschaft für Mathematik
URL: http://schulmatheforum.de/vorkurszettel?id=53
| Dietlind Bäro Daniel Metzsch | www.matheraum.de Mathe für's ABI 2008 Aufgabenblatt 1 Abgabe: Do 15.11.2007 23:00 | 01.11.2007 |
| Aufgabe 1 | ||
| Bearbeiten Sie die Aufgabenteile. Beschreiben Sie dabei Ihre Vorgehensweise und kommentieren
Sie Ihre Lösungen. Die Qualität der textlichen Begleitung wird mitbewertet. 1. Pyramide (Grundkurs) In einem dreidimensionalen, kartesischen Koordinatensystem sind die drei Punkte A(1|1|1), B(3|3|1) und C(0|4|5) sowie die Gerade 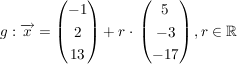 gegeben. gegeben.
a) Die Punkte A, B und C bilden ein Dreieck. Weisen Sie nach, dass dieses Dreieck gleichschenklig ist. Berechnen Sie die Größe der Innenwinkel und den Flächeninhalt des Dreiecks. b) Die Punkte A, B und C sind in einer Ebene E enthalten. Bestimmen Sie eine Koordinatengleichung von E. (Mögliche Lösung zur Kontrolle Ihrer Rechnung: E: x y + z = 1) c) Der Punkt S(6|-2|8) ist die Spitze einer Pyramide mit der Grundfläche ABC. Stellen Sie die Pyramide und die Gerade g graphisch dar. Benutzen Sie dafür das beigefügte Koordinatensystem. Bestimmen Sie das Volumen der Pyramide. d) Untersuchen Sie, ob g die Kante AS der Pyramide schneidet. e) Für jedes Ermitteln Sie eine Gleichung der Schnittgeraden der Ebenen 2. Dach (Leistungskurs) ![[Dateianhang]](uploads/forum/00317853/forum-i00317853-n001.png)
a) Geben Sie für die vier Wandebenen b) Bestimmen Sie das Volumen des Hauses. c) Berechnen Sie die Länge der Antenne von der Spitze M bis zur Dachschräge. d) Untersuchen Sie, ob die Antennenspitze M vom Punkt P(3|1|0) sichtbar ist. e) Die Sonne scheint in Richtung 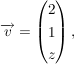 z<0. M' ist der Schatten der Antennenspitze M. Bestimmen Sie die Koordinaten von M′ in Abhängigkeit von z, führen Sie eine sinnvolle Fallunterscheidung durch. z<0. M' ist der Schatten der Antennenspitze M. Bestimmen Sie die Koordinaten von M′ in Abhängigkeit von z, führen Sie eine sinnvolle Fallunterscheidung durch.
Viel Erfolg. Aufgaben entnommen aus: | ||
© Copyright 2003-25 www.schulmatheforum.de
Der Inhalt dieser Seite kann -- sofern nicht anders lautend gekennzeichnet -- durch jedermann gemäß den Bestimmungen der Lizenz für Freie Inhalte genutzt werden.
Der Inhalt dieser Seite kann -- sofern nicht anders lautend gekennzeichnet -- durch jedermann gemäß den Bestimmungen der Lizenz für Freie Inhalte genutzt werden.